A legtöbben rávágnánk, hogy „dehogy!”, és a 17. század végén egy ismeretlen is így fogadott Rajnai Rupert herceggel. Rupert – I. Károly angol király unokaöccse, a polgárháború királypárti fővezére – a windsori laborjában fémekkel és üveggel kísérletezett, és végül ő nyerte a fogadást.

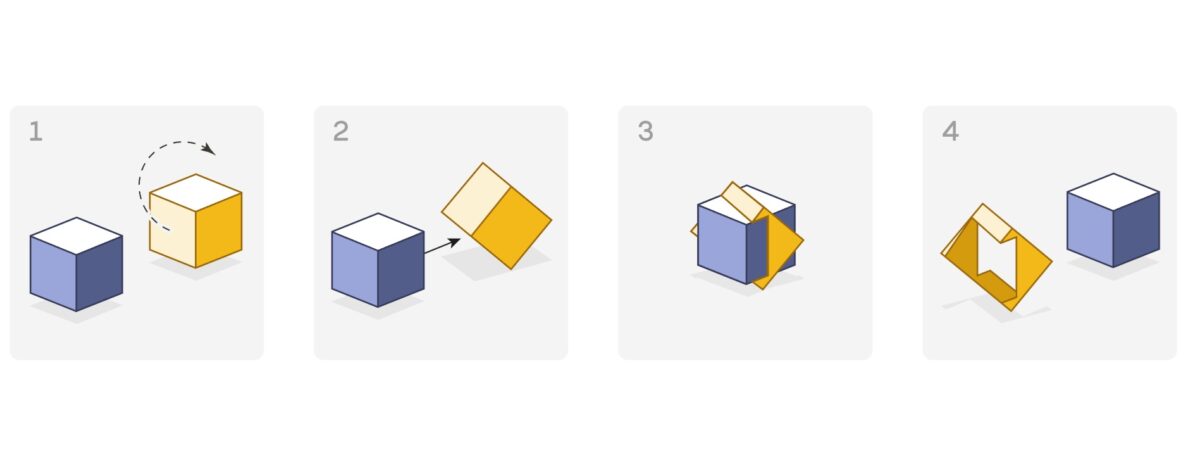
1693-ban John Wallis matematikus leírta, hogy ha a kocka belső átlója mentén fúrunk egy egyenes alagutat, az elég széles lehet ahhoz, hogy egy másik kocka átférjen rajta. Az eredmény azonban szoros: ha a második kocka csak 4%-kal nagyobb, már nem megy át. Adja magát a kérdés: mely más testek tudják ezt a „trükköt”?

Mint kiderült, elég sok. A „Rupert-tulajdonság” számos konvex poliédernél működik (konvex = lapos oldalú, benyomódás nélküli test): 1968-ban Christoph Scriba a tetraéderre és az oktaéderre is kimutatta, az elmúlt évtizedben pedig a dodekaéderre, az ikozaéderre és a focilabda-formára is.

Ezek nyomán kialakult a matematikai sejtés, hogy minden konvex poliéder átenged magán egy másikat.

Most viszont Jakob Steininger (Statistics Austria) és Sergey Yurkevich (A&R Tech) előálltak a „Noperthedronnal”, egy 90 csúcsú, 152 lapú testtel (150 háromszög és két szabályos tizenötszög).

Árnyékvetéses módszerrel, egy „globális” és egy „lokális” tétellel, valamint körülbelül 18 millió beállítás végigellenőrzésével azt is bizonyították, hogy bármilyen egyenes alagutat fúrunk, egy másik Noperthedron nem fér át rajta.

„A természetes sejtést megcáfolták” – mondta O’Rourke.

Vagyis most már tudjuk, hogy léteznek nem Rupert-tulajdonságú testek – és kezdődhet a vadászat a következőkre.

(Kép: A Noperthedron. Mindmáig ez az egyetlen olyan forma, amelyről bizonyították, hogy nem rendelkezik a Rupert-tulajdonsággal)